Posters
Detection and Classification of Historic Watermarks using neural networks and nearest neighbor search
Sebastian Pfaff, Evghenii Beriozchin, Paulina Weyh, Martin Skrodzki, Lena Polke, Ramon Voges
At: Digital Humanities im deutschsprachigen Raum 2024
Handcrafted European papers from the 13th to 19th centuries often feature watermarks. The papermaker added these to make their paper more recognizable. Today these watermarks play a vital role in dating and verifying historical documents, offering valuable insights into paper origins and production. We present a new automated method for finding similar watermarks based on the digitized collections of the German Museum of Books and Writing and the German National Library. Unlike previous approaches, which relied on image processing or neural network classification, our approach utilizes a CycleGAN neural network to generate artificial watermark sketches from scanned historical papers. The sketches are compared using a pre-trained ResNet18 neural network and the Spotify Annoy algorithm for efficient nearest neighbor search in the database. Our pipeline achieves a 63% accuracy in finding similar watermarks within the 50 nearest neighbors from a database of over 6200 photographed watermarks and traced watermarks.
A Watermark Recognition System: An Approach to Matching Similar Watermarks
Martin Skrodzki, Diana Banţă, Sydney Kho, Anna Lantink, Alexandru Marin, Vladimir Petkov
At: Vision and Depiction 2024
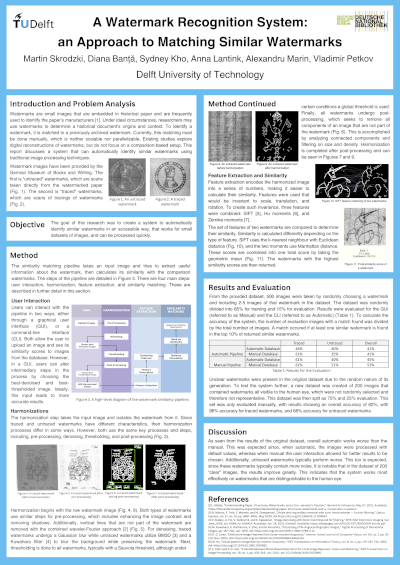
Watermarks are small images that are embedded in historical paper and are frequently used to identify the paper's manufacturers. Under ideal circumstances, researchers may use watermarks to determine a historical document's origins and context. To identify a watermark, it is matched to a previously archived watermark. Currently, this matching is performed manually. The goal of this research is to create a system to automatically identify similar watermarks in an accessible way, that works for small datasets of images, and can be processed quickly.
Holonomy
Scott Jochems, Joris Rijsdijk, Ravi Snellenberg, Rafael Bidarra, and Martin Skrodzki
At: Vision and Depiction 2024
This poster presents a a virtual reality game in which a player attempts to navigate through a hyperbolic space while staying within a 3x3 meter Euclidean space.
Isotropic Point Cloud Meshing using unit Spheres (IPCMS)
Henriette Lipschütz, Ulrich Reitebuch, Konrad Polthier, and Martin Skrodzki
At: International Geometry Summit 2023
This poster presents an algorithm to derive triangle meshes from unstructured point clouds. The occurring edges have a close to uniform length and their lengths are bounded from below. Theoretical results guarantee the output to be manifold, provided suitable input and parameter choices. Further, the paper presents several experiments establishing that the algorithms can compete with widely used competitors in terms of quality of the output and timing. Furthermore, the output is stable under moderate levels of noise.
Explorative Analysis via t-SNE Visualization of High-Dimensional Data
Martin Skrodzki
At: Hausdorff Summer School on Algorithmic Data Analysis
The t-SNE algorithm provides a means to visualize high-dimensional data sets as two-dimensional point clusters. We present the algorithm, its underpinning mathematical concepts, and directions for future research.
Visually-guided investigations of sub-structures in 3D Turing-like patterns
Martin Skrodzki, Ulrich Reitebuch, and Eric Zimmermann
At: The 22nd RIKEN Interdisciplinary Exchange Evening, 25 September 2020, Wako-Shi, Japan (online)
Turing proposed a reaction-diffusion model for skin coloring, which was subsequently discretized by Young as a cellular automaton. We investigate the parameter space of the automaton as well as the distribution of the corresponding 3D patterns.
Online Geometry Visualization Frameworks – A Case Study
Martin Skrodzki
At: Geometry Labs United Workshop, 17-18 Juli 2020, Providence, RI, USA (online)
The JavaView visualization framework was designed at the end of the 1990s as a software that provides—among other services—easy, interactive geometry visualizations on web pages. Subsequently, it was widely used in geometry groups around the globe. However, as JavaView’s easy web exports was based on Java Applets, the deprecation of this technology disabled one main functionality of the software. This poster summarizes the main findings of a case study centered on the JavaView software.
Large-scale Evaluation of Neighborhood Weights and Sizes
Martin Skrodzki and Eric Zimmermann
At: SMI and SPM Conference, 2-4 June 2020, Strasbourg, France (online)
We investigate the quality of weighted neighborhoods with different sizes. The weights are determined by the normal similarity between points and are given by a sigmoid function modeling both continuous and sharp increases. Our large-scale analysis consists of more than 1,000 point sets.
Velimir Khlebnikov's Laws of Time
Henriette Lipschütz, Ulrich Reitebuch, and Martin Skrodzki
At: Illustrating Dynamics and Probability Workshop, 11 - 15 November 2019, Providence, RI, USA
The artist Kristina Paustian honored the Russian futurist Velimir Khlebnikov with her solo exhibition \emph{Laws of Time. The future calculations by Velimir Khlebnikov} in Berlin, Germany. Amongst other aspects, she focused on his poetry and the mathematics used in his works. On this poster, we investigate his “Laws of Time” and motivate a subsequent question in probability.
Processing of Point Set Surfaces
Martin Skrodzki, Eric Zimmermann, Ulrich Reitebuch, Sunil Yadav, and Konrad Polthier
At: Illustrating Geometry and Topology Workshop, 16 - 20 September 2019, Providence, RI, USA
Point Sets are acquired as representations of surfaces in R3 e.g. via laser-scanning or LiDaR. At first, they are unstructured and neighborhood relations have to be established. Then, noise added during generation has to be removed robustly also on non-uniform input while retaining features. The obtained cleaned point set can then be used for e.g. surface reconstruction and subsequently for 3D printing.
Variational Shape Approximation of Point Set Surfaces
Martin Skrodzki, Eric Zimmermann, and Konrad Polthier
At: IGS 2019 International Geometry Summit, 17 - 21 June 2019, Vancouver, Canada
Awarded the “Best Poster Award”
This work proposes an algorithm for point set segmentation based on the concept of Variational Shape Approximation (VSA), which uses the k-means approach. It iteratively selects seeds, grows flat planar proxy regions according to normal similarity, and updates the proxies. It is known that this algorithm does not converge in general. We provide a concrete example showing that the utilized error measure can indeed grow during the run of the algorithm. To reach convergence, we propose a modification of the original VSA. Further, we provide two new operations applied to the proxy regions, namely split and merge, which enqueue in the pipeline and act according to a user-given parameter. The advantages over regular VSA are independence of both a prescribed number of proxies and a (manual) selection of seeds. Especially the latter is a common drawback of region-growing approaches in segmentation.
Velimir Khlebnikov's Laws of Time
Henriette Lipschütz, Ulrich Reitebuch, and Martin Skrodzki
At: Art exhibition “Laws of Time. The future calculations by Velimir Khlebnikov”, 16 - 23 March 2019, Feldfünf, Berlin, Germany
The (video) artist Kristina Paustian honored the Russian futurist Velimir Khlebnikov with her solo exhibition “Laws of Time. The future calculations by Velimir Khlebnikov” in Berlin, Germany. Among other aspects, she focused on his poetry and the mathematics used in his works. In this paper, we present the connections of Khlebnikov's writings to mathematics and his thoughts about foretelling the future by analyzing several events which took place in the past. On this poster, his ideas are visualized and evaluated in comparison to randomly generated data.
Analysis of NVT-based Point Set Denoising in Parameter Space
Eric Zimmermann, Sunil Yadav, Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
At: SMI 2018 Conference, 6 - 8 June 2018, Lisbon, Portugal
Our point set denoising algorithm is an iterative, three-phase algorithm for noisy point sets. Its parameters offer a variety of tuning opportunities. Used models are the gargoyle (real, noisy, irregular), the Chinese ball (real, noisy, many features) and rabbit (real, noisy, many features), the fan disk (synthetic, noisy, sharp features, near-flat areas), the sphere (synthetic, noisy), and the cube (synthetic, noisy, sharp features). We compare the effect of different parameter values on the obtained result as well as on the number of iterations taken by the algorithm.
Asymptotical & Combinatorial Results on the Neighborhood Grid Data Structure
Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
At: Einstein Workshop Discrete Geometry and Topology, 13 - 16 March 2018, Berlin, Germany and Workshop Mathematics and Image Analysis 2018, 15 - 17 January 2018, Berlin, Germany
The Neighborhood Grid approximates neighborhood information. A (quadratic) matrix contains the coordinates of the points such that in each row the x-values are increasing while in each column the y-values are increasing.
For the algorithm, the order of the points suffices, the exact coordinates are irrelevant. If the above ordering is given, we call it a “stable state”.
We provide both an upper and a lower bound on the building time for such a stable state. Furthermore, we present some combinatorial results on open research questions concerning the data structure.
Computational and Structural Aspects of Point Set Surfaces
Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
At: BMS Days 2018, 19 - 20 February 2018, Berlin, Germany
The Neighborhood Grid approximates neighborhood information. A (quadratic) matrix contains the coordinates of the points such that in each row the x-values are increasing while in each column the y-values are increasing.
For the algorithm, the order of the points suffices, the exact coordinates are irrelevant. If the above ordering is given, we call it a “stable state”.
We provide results on the convergence of a parallel building algorithm for stable states. Furthermore, we investigate the uniqueness of stable states.
Computational and Structural Aspects of Point Set Surfaces
Martin Skrodzki and Ulrich Reitebuch
At: SIAM Conference on Industrial and Applied Geometry, 8 - 13 Juli 2017, Pittsburgh, USA
Based on previous, well-established, and successfully used discretization schemes of differential geometric structures and operators on triangulated meshes, we take the next step and transfer this calculus to point set surface data. These arise naturally in 3D acquisition processes. We aim at a theoretical framework, which mimics a many features as possible of smooth manifolds in the setting of point sets.
The Neighborhood Grid approximates neighborhood information. A (quadratic) matrix contains the coordinates of the points such that in each row the x-values are increasing while in each column the y-values are increasing.
For the algorithm, the order of the points suffices, the exact coordinates are irrelevant. If the above ordering is given, we call it a “stable state”.
We provide results on the convergence of a parallel building algorithm for stable states. Furthermore, we investigate the uniqueness of stable states.
Computational and Structural Aspects of Point Set Surfaces
Martin Skrodzki
At: BMS Days 2017, 20 - 21 February 2017, Berlin, Germany
Based on previous, well-established, and successfully used discretization schemes of differential geometric structures and operators on triangulated meshes, we take the next step and transfer this calculus to point set surface data. These arise naturally in 3D acquisition processes. We aim at a theoretical framework, which mimics a many features as possible of smooth manifolds in the setting of point sets.
